An
Emergent Origin or Semiotic Functionality: Symmetry, Objective Relational
Levels, and Inference of Novel Logical Categories in a Connectionist System
Dario Nardi, Adjunct Assistant Professor, Program in Computing
University of California, Los Angeles
Abstract-
One
simple type of connectionist system, the Fuzzy Cognitive Map (FCM), produces
patterns of dynamical output with three important structural properties and
capabilities: symmetry, objective relational levels, and the automatic
inference of novel logical categories. Together, these emergent properties
also reveal a connectionist system that, when cast in the role of a learning
agent, has the power to experiment with and discern relevant from trivial
information in the environment. This functional form of autonomy also
demonstrates that Connectionism can meet at least some of the criteria for
creating a truly autonomy system. This “FCM process” also opens the way
for a variety of interesting and powerful applications.
Introduction
Controversies
around the properties and capabilities of any basic paradigm such as
Connectionism can benefit from new discoveries, and as with any piece of new
news, new questions arise that were previously unimagined or neglected. This
on-going discovery-with-new-questions phenomenon is one aspect of the endless
cycle called the scientific method. This phenomenon is also, in a way, the
topic of this paper: armed with new capabilities, one kind of connectionist
system called the Fuzzy Cognitive Map is now equipped to handle some of the
more complex on-going processes like this one.
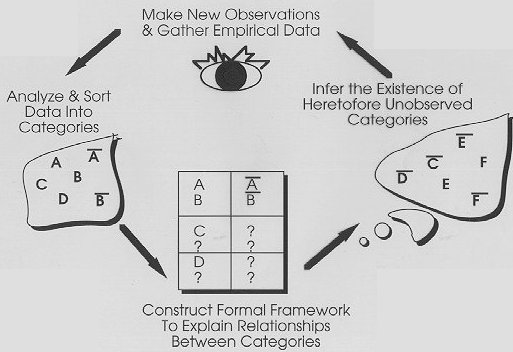
Figure
1: A semiotically closed (autonomous) process
The metaphor
merely serves the purpose of explaining, by analogy, the novel FCM properties
to be explored here: a Connectionist system that, "on its own," is
capable of generating the necessary internal structures.
(The complete story of discovering the elementary particles if of
course far more involved.)
In brief, the attractor basins of the FCM are related to each other structurally in the form of relational hierarchies. Symmetry, objective relational levels, and the inference of novel logical categories emerge as patterns in FCM output. Further, this autonomous closed-loop cycle between the environment and computation suggests "semiotic closure." Just as genetic information in the context of environment includes syntax, semantics and pragmatics in one closed-loop package for biological systems, so too does this functional process describe a cyclical flow that includes some – not all – of the best properties of classic AI, connectionist and situated action systems.
The
Fuzzy Cognitive Map
Bart Kosko developed the Fuzzy Cognitive Map as a connectionist approach to holistically evaluating expert advice and insights into complex, or non-linear, everyday human activities such as politics, economics and social behavior. Since its introduction, a number of FCMs have been created on topics ranging from Aparteid in South Africa to the French Revolution and dolphin behavior. Figure 2 is a typical FCM. One application of the FCM in particular that has been well developed is modeling virtual systems – in a virtual reality environment, for example, the FCM is used to simulate the non-linear behavior of the variables in that virtual environment.
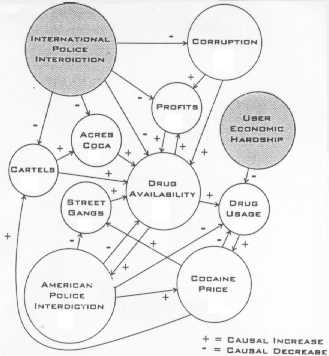 Figure
2: An example FCM
Figure
2: An example FCM
FCMs are generally "hand-made." Experts are consulted on a particular topic, pertinent variables and factors become FCM nodes, and links between nodes (edge weights) are established based on the experts’ observations of "causal" relationships between the variables. Variables may vary together, or vary inversely, or not vary together at all. Node states and edge weights can be "black or white," or take on fuzzy numeric values. And unlike more common connectionist systems like neural networks, FCMs do not have discrete input and output nodes. The input to the system is the set of initial states for all nodes, while the output for the system is the set of node states after the system has been iterated and "settles down." Figure 3 is a generalized Fuzzy Cognitive Map.
Once created, the FCM is fed with a set of initial conditions and the FCM's nodes and links are evaluated simultaneously. For example, if the topic is dolphin behavior, then as one variable such as hunger increases (the node labeled "hunger level" takes on an "up" state) then the search for food is pushed to increase (the node labeled "hunger level" takes on an up state.) Naturally, with many interacting variables, the "hunger level" may or may not increase, immediately or ever, depending on the effects of other nodes. That a single causal effect may never show up under one set of initial conditions is an important distinction between the FCM and a hard-and-fast rule-based "expert" system.
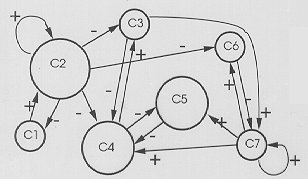 Figure
3: An abstract FCM
Figure
3: An abstract FCM
| Time | Features
(Nodes with positive node states) |
| 4 5 6 7 8 9 10 |
International
Police Interdiction, US Police Interdiction, Cocaine Price US Police
Interdiction, Cartels, Acres Coca, Corruption Profits,
Drug Availability, Drug Usage International
Police Interdiction, US Police Interdiction, Cocaine Price US Police
Interdiction, Cartels, Acres Coca, Corruption Profits,
Drug Availability, Drug Usage International
Police Interdiction, US Police Interdiction, Cocaine Price |
Table 1: Sample FCM Output from the “War on Drugs”
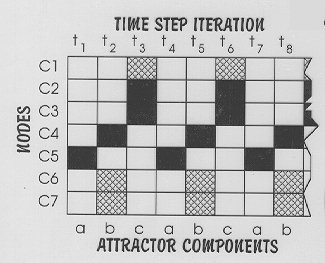 Figure
4: FCM iteration gives limit cycles.
Figure
4: FCM iteration gives limit cycles.
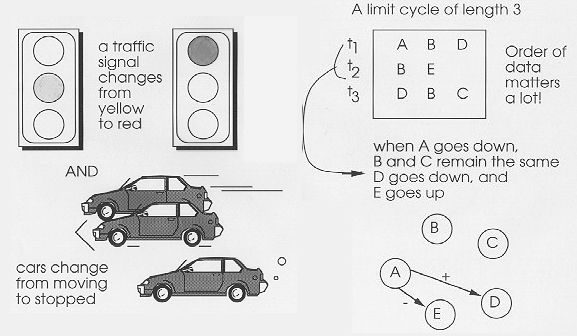
And the FCM is repeatedly iterated, each iteration producing an "attractor component" (a set of node of node states at a single time interval "t.") After a number of iterations the system output usually repeats, revealing a limit cycle (a fixed point attractor, strange attractor or chaos is possible.) Further, just as one particular set of initial conditions may produces a one limit cycle, a different set of initial conditions may produce the same limit cycle or another different limit cycle. Figure 4 shows typical FCM output. A word about notation here: “black” indicates an “up” state, “checkered” indicates an “intermediate” state, and empty “white” indicates a “down” state.
Not all FCMs are hand-made. Presented with a set of observations over a period of time, a blank-slate FCM can be trained to set edge weights that reflect observed "causal" relationships. After this training, when the FCM is iterated from a set of initial conditions, the output mirrors the earlier observed "training set." This learning method, called "Differential Hebbian Learning," calculates edge weights by looking at how observed variables change together over time. A generic example with simple graph of this method is shown in Figure 5.
 Figure
5: Differential Hebbian learning
Figure
5: Differential Hebbian learning
For the example dolphin FCM mentioned above, the FCM in training observes that as "dolphin hunger" increases then "food searching" also frequently increases, suggesting co-variance of the two variables. Naturally, hunger may not always lead immediately to food searching, as other variables such as "sharks present" may overcome the strength of the "causal" relationship. This is similar to the logic: "All other things being equal, such-and-such rule applies." This training method, when coupled with the usual tweaking techniques, produces surprisingly faithful output.
Three Novel FCM Properties
The dynamic outputs (as in Figure 4) of a large number of hand-made and randomly generated FCMs, ranging in size from seven to twelve nodes, were explored. For each FCM, a set of randomly generated initial conditions were fed in, and the resulting iterated output recorded. This was repeated two hundred times for each FCM. A variety of output was generated: some FCMs had few limit cycles, others many; some limit cycles were short while others were long, up to twenty-two time units; many FCMs produced a variety of short and long limit cycles.
Trivalent edge weights and node states were used (-1, 0, +1.) Other combinations of bivalent and trivalent states such as (0,1) and (0,0.5,1) did not produce the results discussed below. This three-value logic allows for fuzzy variable states: for any given category defined by an attractor basin, some features will be noted for there presence (+1) and others by their absence (-1), while some features (0) will not play a part, or play an undetermined part, in defining the category. Although a crisp two value logic of (-1,+1) did produce an impoverished kind of symmetry, it did not produce the "interesting" range of complexity and all three of the emergent properties seen here.
Finally, an arbitrary coding system was used to simplify the cataloguing of the attractor components and limit cycles born from the random initial conditions fed to each FCM. A two-part address, exponent-based coding scheme was used. For example, Table 2 shows the calculation of the address of an eight-node FCM attractor component.
|
Step 1 |
Node
states at time "t" |
{-1,0,0,+1,+1,-1,0} |
| Step
2 |
Exponent
Translation |
{24+25,-21-27} |
| Step
3 |
Final
two-part address |
{+48,-130} |
Table 2: Arbitrary limit cycle coding scheme
This coding method insures that all attractor components receive a unique address. It is otherwise arbitrary, used to eliminate the need for thousands of visual inspections. A sample limit cycle of length four (four attractor components) is shown in Table 3.
| Time Step Iteration | Component
Address |
Relational
Label |
Each
attractor component is a set of node states at time iteration
"t" |
| 1
2 3 4 |
(+88,
-6) (+26,
-64) (+6,
-88) (+64,
-26) |
a
b NOT a NOT b |
{0,-1,-1,+1,+1,0,+1} {+1,0,0,+1,+1,-1,0} {0,+1,+1,-1,-1,0,-1} {-1,0,0,-1,-1,+1,0} |
Table 3: "Self-complementary" limit cycle A
Limit cycles such as this one exhibit symmetry between their components. This type of limit cycle will be called "self-complementary." Other limit cycles, such as the four additional ones shown in Table 4, are not self-complementary but "pair-wise complementary:"
| Limit Cycle B | Limit
Cycle Not-B |
Limit Cycle C | Limit
Cycle Not-C |
| (+6,-102) (+54,-150) (+18,-20) (+2,-76)
|
(+102,-6) (+150,-54) (+20,-18) (+76,-2)
|
(+99,-10) (+90,-12) (+17,-100) (+144,-50) (+2,-15) (+22,-55) |
(+10,-99) (+12,-90) (+100,-17) (+50,-144) (+15,-2) (+55,-22) |
Table
4: "Pair-wise complementary" limit cycles
The pair-wise
complementary limit cycles in Table 4 have been kept simple to illustrate the
phenomenon with a minimum of fuss: limit cycles with a dozen or more attractor
components abound. Note that the
“B family” is has four components while the “C family” here has six.
A single FCM may have both pair-wise complementary and self-complementary limit cycles, and all FCMs with trivalent node states (-1,0,+1) appear to exhibit this symmetry phenomenon.
A corollary phenomenon is also possible: one of the attractor components in Limit Cycle pair C / Not C might also appear in Limit Cycle pair B / Not B. The appearance of this corollary phenomenon varies with the FCM. Some FCMs exhibit no duplication of component attractors, while others have many duplications. The meaning and importance of this is illustrated by an example. If node states stand for the presence or absence of certain animal features, for example, then a particular combination of features (say, an endocrine system) can be the same in two different animals while another combination of features (say, mode of locomotion) could be completely different. The graphical representation of the FCM output, in Figure 6, reveals the presence of symmetry at three levels – the attractor component level, the limit cycle level, and the kind-of-symmetry level. These levels of symmetry generate objective relational levels.
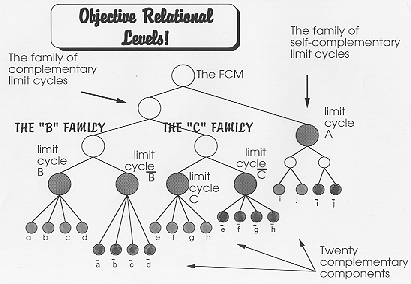 Figure
6: Relational levels
Figure
6: Relational levels
The levels found in the FCM output are only one kind of hierarchy. Other hierarchical structures such as those found in human organizations like bureaucracies have some elements sitting above or below others, where for example, a dean sits above department chairmen, who sit above individual professors, and so on. In contrast, the levels generated by the FCM are relational, like the levels found in natural language, where all the elements sit at the same level but fall into different hierarchically related categories.
These relational patterns in FCM output were discovered by, and have been described mostly in terms of, iterated "time step" output or graphs like Figure 6. This is not truly reflective of the underlying mathematics, however. The FCM patterns are attractor basins and thus the relational patterns are ultimately geometric in nature: cycles in space instead of in time, graphs on a surface with no particular beginning or end. This has important consequences to be discussed later.
 Figure
7a: Example distribution of novel logical categories
Figure
7a: Example distribution of novel logical categories
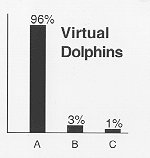
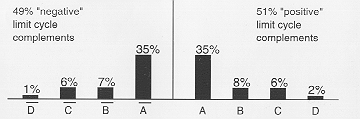
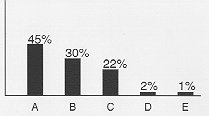
Finally, the automatic inference of novel logical categories emerges out of the FCM training process. With the dolphin FCM mentioned above, for example, the training process will get the FCM to reproduce the limit cycle trained for, but only under a certain range of initial conditions. Other initial conditions may produce different limit cycles not trained for – limit cycles that are not merely random but that obey the symmetry and relational-levels phenomena observed above. Per Figure 7a, the dolphin FCM produces the limit cycle it was trained (A) for 96% of the time, but under certain conditions it will produce two additional self-complementary limit cycles (B and C). If the limit cycle trained for had not been self-complementary, then a pair-wise complement would have been produced at least some of the time, as in Figure 7b.
 Figure
7b: A fully pair-wise complementary FCM
Figure
7b: A fully pair-wise complementary FCM
 Figure
7c: A fully self-complementary FCM
Figure
7c: A fully self-complementary FCM
The distribution of eight limit cycles in figure 7b is indicative of a "fully pair-wise complementary FCM." Each and every limit cycle has a complement. This case, with complements appearing with equal distribution, is a typical pattern in FCM output. Figure 7c is also typical, with five self-complementary limit cycles, and together the three distributions in figure 7 sum up the most common patterns observed. Thus, not all limit cycles appear with the same frequency. With any given FCM there is an interesting distribution of how often certain limit cycles appear.
In short, for each attractor component, some complement necessarily exists somewhere, in the same limit cycle or another limit cycle, but the limit cycles themselves may be either self-complementary (and thus unique) or pair-wise complementary.
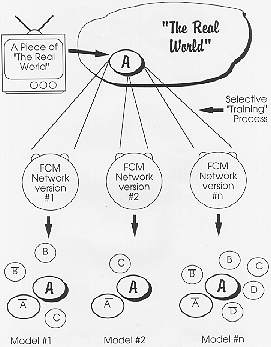 Figure
8: FCM Training and inference
Figure
8: FCM Training and inference
Further, as Figure 8 illustrates, different training instances – different contexts – will reproduce the same "hard" training observations in the FCM output, but not necessarily the same inferences. Alternatively, when training is imperfect, different training may cause the FCM to reproduce difference "hard" observations but make similar inferences. Thus, different training contexts may infer different novel categories, as one might expect from a constructivist view-point. This is possible because, while all attractor components have complements, not all limit cycles do. So the phenomenon of complementarity is not a straight-jacket. This is an important feature that provides a phenomenon expected in semiotically closed systems: two scientists could come up with two different theories to explain the same set of observations, but over the course of multiple contexts – re-infer, re-experiment, re-observe and re-theorize – the "true" (best fit) theory will likely emerge.
Putting together inference with symmetry and objective relational levels, we discover an interesting connectionist system. Aside from the earlier metaphor above the particle physicist’s search for quarks, a number of other intriguing and not so far-fetched applications come to mind in light of the FCM's new found capabilities:
A psychologist, having observed several categories of psychological behavior in subjects, might wonder what other categories could also exist – either potentially or in actuality. Given two training categories, for example, the FCM can infer the two "hidden" categories, to complete the picture. This is more than many psychological studies do, and might even contribute to detecting inconsistencies in existing theories, to modify or help reorganize mismatched features.
The process of natural selection in tandem with structural constraints has generated millions of species on creatures – what other species, currently unknown, unimagined or non-existent, might also evolve given a different set of initial environmental conditions?
Virtual reality and artificial life environments can produce more realistic behavior through the modeling of real world systems. This can be critical when the virtual environment most adapt to the user's actions and interests in ways that are unexpected, or that incorporate new information from the user not originally pre-programmed.
In general, numerous areas of science and mathematics rely on non-arbitrary "theory taxonomies" to organize concepts coherently and suggest new areas of research. "What's missing" is a basic question with a wide variety of applications at the most abstract levels of thought.
Generalizing, a system need no longer make random searches of its environment or rely from the start on pre-programmed heuristics, but search for and test its environment based on hypotheses grounded in a logically constrained imagination.
Even more importantly, however, is the "portability" of FCM relational structures. As often seen in the course of scientific work, once a general and robust theory has been developed, it can be applied to other areas of inquiry. Sometimes the borrowed theory provides tremendous insight and information. Other times it provides little value or perhaps simply a framework to start from – the process of fleshing out the entire pattern generated by an FCM may take a while, and existing training procedures such as Differential Hebbian Learning are mediocre: effective but time-consuming like most connectionist methodologies. Training times are not appropriate for ad-hoc category learning and ad-hoc novel category generation, although the speed at which humans perform these tasks are not notably quick, and ad-hoc learning in many applications may certainly be possible with continuing technological advancements. On the other hand, Table 5 reminds us of a striking and spurious and humorous parallel.
|
Twelve quantum particles |
Four
particle families |
Three
particles in each family, one each positive, negative, and neutral |
| Twelve
signs of the zodiac |
Signs
grouped into four elements (water, air, etc.) |
Three
signs per element, one each positive, negative, and neutral |
Table 5: The danger of FCM theoretic portability
Thus, theoretic portability is not meant to imply underlying universal truths, but that intelligent systems can and likely will find (or "construct") structural and relational similarities between radically different contexts, and these similarities can be the basis for efficiency, creativity or superstition. These kinds of possibilities require a closer look at the broad picture and issues associated with knowledge representation.
Semiosis, Emergence & Autonomy
The questions of knowledge representation are part of larger area: semiotics. In a very general way, at least when applied to “knowledge engineering,” semiotics can be defined as the "theoretical field which analyzes and develops formal tools of knowledge acquisition, representation, organization, generation and enhancement, communication and utilization." The focus here, however, is the circular or "autopoetic" semiotic process, or "semiosis," and the three domains of semiotics: syntax, semantics and pragmatics. The semiotic circle says that a system must be in touch with the world and objects and events in the world, and it must have sensors for perception, and a way to process organization and interpret knowledge, and also include the implementation of knowledge and generation of behavior in the world. Thus, specific criteria must be met for a system to qualify as “semiotically complete,” and a variety of qualifiers have appeared related to semiosis, such as "autonomous," "open-ended," "constructive" and "emergent." Semiotically complete here means a system which includes all three aspects: syntax, semantics and pragmatics.
| Syntax | Semantics | Pragmatics |
| Events in the world are encoded by sensors in a symbolic form, and syntax is symbol manipulation rules. | Interpretation of what the symbols stand for is necessary, in order to formulate relevant behavior. | Knowledge is generated, behavior is tested, artifacts made, and changes implemented in the world. |
Table 6: The three domains of semiotics as applied to knowledge engineering
In biological systems, semiotic closure means symbol driven (DNA) construction of a system for open-ended evolution of that system, where the "speed and fault tolerance of the biological system’s functions are largely a result of the constructive power of the symbols rather than their explanatory power." There is both discrete representation and control (DNA), and the dynamics driven behavior typical of bio-chemically based systems. And the symbols and symbol driven functions are not simply predefined and closed off from the environment, but themselves open to evolution. So there is emergence as a result of natural selection, where environmental conditions play a powerful role. A biological system is more than "autopoetic:" it has boundaries which it forms for itself, and the system consists of components that operate mechanically and are constructed from more elementary components in the environment.
The claim here is that there are non-trivial "emergent" properties that appear from the dynamic output of the FCM, a connectionist system. From one perspective, emergence refers to the appearance of a novel structure or function, usually from a self-organizing dynamic system – a system which generates new patterns, structures, functions and so on from existing components and initial and boundary conditions.
From another perspective, emergence refers simply to "autonomous organization," a system which acts according to its own references or model of behavior in spite of inputs from the environment, yet depends on those inputs, perhaps many environmental inputs, in formulating its behavior. From either view, to claim complete semiotic closure, the FCM driven system must be interactive with the world, with symbols (feature labels) and symbol driven processes that are open to change with respect to both the environment and its own existing internal representations. This is a tall order.
Connectionist systems of all kinds can store categories – the potential of the observations reported here expands on current applications in categorization and control mechanisms and introduces a process for connectionist systems to search their environment in a logical (relational) way without relying exclusively on explicit (syntactic rule-based) heuristics.
- Rule-Based Symbolic AI vs. Distributed Connectionist AI
- AI as Embodied Situated Action vs. AI as Disembodied Mind
The relational properties of FCM output provide a simple kind of open-ended syntax, where categories are based on both particular micro-features and relationships between micro-features and between categories. At a second vertex, the FCM possesses many of the dynamics and flexibility of connectionist systems – superficially, the FCM is not the well-known neural network, with linear processing from inputs through hidden layers to outputs. Nonetheless, as a connectionist system, it is both dynamic in output and statistical in design, with the FCM acting as a processor with inputs from "outside" the system and patterns in its outputs. The third vertex provides important benefits of "situated action," which posits that learning, as opposed to inferencing, occurs only with respect to an environment. Further, the theoretical structures generated by the FCM emerge from patterns in its output, given repeatedly different kinds of input (different contexts.) And this output might be represented by ad-hoc symbols in the "mind" of the system, or might be represented by physical concrete symbols created or arranged by the system (as a robot) in its environment (such as a robot arranging multi-colored blocks in groups to represent different categories). Together, many desirable features are combined into a system that can be a semiotically-closed system that includes the syntactical, semantic and pragmatic functions that these three different approaches provide to intelligent systems.
Several important curiosities and issues come to mind. What affect does this or that specific training procedure have on the inference of novel categories? Do different training algorithms generate radically different inferences? Or is there something inherent in the structure of the FCM that more-or-less fixates this phenomenon? This connects with the question: why are only trivalent node states effective in generating these emergent properties? Intuitively, the geometric nature of the FCM, in tandem with principles like transitive closure, suggest a mathematical proof, while research by others shows "combinatorial structural features" found in the attractor basins of some dynamic systems. Further, although the hierarchical structure of the FCM output resembles the tree-structures typical of natural language, the FCM output is cyclical (in time) or geometric (in space) while language is linear. One neurological theory is that different areas of the brain coordinate language through phase matching (areas of the brain in-phase with each other are linked together.) The idea of phase may be compatible with FCM cyclical behavior. Or it may not. A critical feature of human language processing, in comparison to language use by lower animals like apes, is proper sequencing, where ideas (subjects, objects, verbs) are grouped together in a way that makes sense. The proper stringing together of elements (subjects always first, for example) is a level of syntax unique to humans. This suggests that the properties and capabilities explored here, while rich for a number of applications, are not rich enough to capture the Holy Grail of language. These issues are the province of future investigation.
Nonetheless, as often occurs, even a minor new discovery can impact the nature of a debate. To date, connectionist systems have been critiqued as lacking, in a fundamental way, some of the basic "structural" features needed to handle certain problems. For example, there is a difference between a symbol described implicitly in terms of a pattern of micro-features, and a symbol defined according to a syntax of functions and hierarchically defined sub-symbols. The hierarchical nature of FCM output brings Connectionism closer to this and other capabilities that are more closely associated with classical rule-based systems. And in a completely different vein, the importance of relevance and the FCM's categorization-modeling- inference-experimentation cycle strengthens connections to a critical concept in situated action: learning as adaptation to the environment. Together, the play between syntax, semantics and pragmatics – structured information processing within an environment – means that the emergent properties of the FCM are not mere curiosities but a foundation for an autonomous intelligent agent.
Finally, the model of the modeling process presented as a metaphor here to explain Fuzzy Cognitive Map behavior is more than a metaphor – it comes out of a larger tradition of thinking about the modeling process – that is, meta-modeling. Experience suggests that there are several paths to chart one’s progress in the pursuit of research, novel discoveries, and the development of new ideas. One of these paths is the FCM modeling process. Conversely, experience also suggests that for something to be purely novel there cannot be a predictable process – everything will be different. In this sense, there is no model, not even a meta-model. This notion of modeling the research process also acts as a bridge between where we have just been and where we’re headed next. In trying to get a handle on artificial intelligence (AI) from an interactive, semiotic, autonomous point of view, are models of the modeling process arbitrary? Are there guiding principles or a framework for dealing with such issues as contradiction, incompleteness of information, and multiple hierarchical levels in systems, in addition to semiosis, emergence and autonomy?
References
Amit,
D.J. Modeling Brain Function: The World of Attractor Neural Networks.
Cambridge: Cambridge university Process, 1989.
Baker,
G. L., & Gollub, J. P. Chaotic Dynamics: An Introduction. Cambridge:
Cambridge University Press, 1990.
Beale,
R. & Jackson, T. "Neural Computing: An Introduction."
Philadelphia: IOP Publishing Ltd, 1990.
Beer,
R. D. “A dynamical systems perspective on agent-environment interaction.”
Artificial Intelligence, 72, 173-215. 1995.
Dayhoff
, Judith. "Neural Network Architectures." New York: Van Nostrand
Reinhold, 1990.
Kelso,
J. A. S. Dynamics Patterns: “The Self-organization of Brain and Behavior.”
Cambridge MA: MIT Press.
Kosko,
Bart & Dickerson, J.A.. "Virtual Worlds as Fuzzy Cognitive
Maps." Presence, vol.3, no.2, 1994.
Kosko,
Bart. "Fuzzy Thinking: The New Science of Fuzzy Logic." New York:
Hyperion, 1993.
Kosko,
Bart. "Neural Networks and Fuzzy Systems: A Dynamical Systems Approach to
Machine Intelligence." Eaglewood Cliffs, NJ: Prentice Hall, 1992.
Massaro.
"Some Criticisms of Connectionist Models of Human Performance."
Journal of Memory and Language, v27., 1988.
Neissel,
Ulric , Ed. "Concepts and Conceptual Development." Cambridge:
Cambridge University Press, 1987.
Noelle,
D. C., & Cottrell, G. W. “In search of articulated attractors.” In G.
W. Cottrell ed., Proceedings of the 18th Annual Conference of the
Cognitive Science Society. Mahwah: Lawrence Erlbaum, 329-334, 1996.
Pattee,
Howard H. “Evolutionary Strategies of Semiotic Modeling and Control.”
Workshop on Control Mechanisms for Complex Systems Issues of Measurement and
Semiotic Analysis. Las Cruses, NM, 1996.
Port,
R. & van Gelder T, ed. Mind as Motion: Explorations in the Dynamics of
Cognition. Cambridge MA, MIT Press, 1995.
Quinlan,
Philip. "Connectionism & Psychology." Chicago: The University of
Chicago Press, 1991.
Van
Mechlen, Iven, Ed. et. al. "Categories and Concepts: Theoretical Views
and Inductive Data Analysis." San Deigo: Academic Press, 1993.
Wisniewski, E. & Medin, D. "On the Interaction of Theory and Data in Concept Learning." Cognitive Science, v.18 No.2 Apr-June, 1994.
This paper is published as Part I of dissertation: "Thinking Systems: A Systems Approach to the Computer as an Extension of the Mind."